Difficulty level:
High-school physics. |
Spring and Rope Puzzle
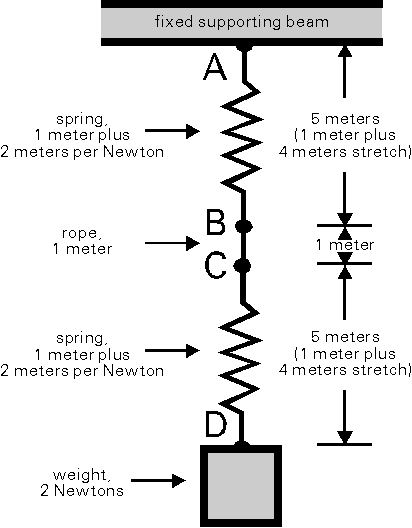 A weight is suspended from a fixed support by two springs and some rope as
shown in the diagram to the right
(click image for larger view). The
weight is two Newtons. (If you aren't metric, use pounds and feet instead of
Newtons and meters; the problem will work the same.) Each spring is one meter
long when unstretched, and it stretches two meters for every Newton of force on
it. The rope from B to C is one meter. Like all textbook physics problems, this
one uses ideal parts. In particular, the springs and ropes have no mass of
their own.
A weight is suspended from a fixed support by two springs and some rope as
shown in the diagram to the right
(click image for larger view). The
weight is two Newtons. (If you aren't metric, use pounds and feet instead of
Newtons and meters; the problem will work the same.) Each spring is one meter
long when unstretched, and it stretches two meters for every Newton of force on
it. The rope from B to C is one meter. Like all textbook physics problems, this
one uses ideal parts. In particular, the springs and ropes have no mass of
their own.
The two-Newton weight stretches each spring by four extra meters, making each
spring five meters long in total. So the distance from A to D is five meters of
spring plus one meter of rope plus five meters of spring, for a total of eleven
meters.
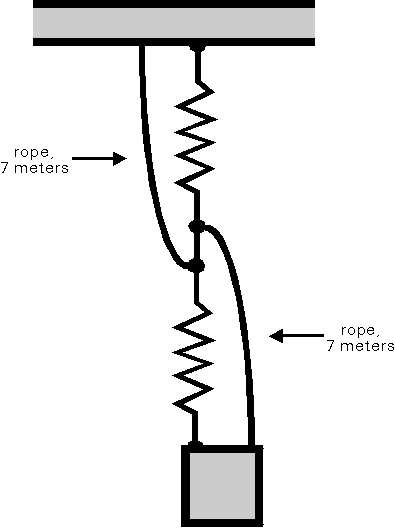 Also note that the distance from A to C is six meters, and the distance from B
to D is six meters. This is important because we are going to connect seven
meters of rope from C to a point near A, and from B to a point near D. Since
each rope is longer than the six meter distance, the rope hangs slackly. The
new ropes are shown to the left (click
image for larger view).
Also note that the distance from A to C is six meters, and the distance from B
to D is six meters. This is important because we are going to connect seven
meters of rope from C to a point near A, and from B to a point near D. Since
each rope is longer than the six meter distance, the rope hangs slackly. The
new ropes are shown to the left (click
image for larger view).
Now here is the question: What happens when you cut the one-meter rope from B
to C? This rope is helping hold up the weight, so the weight will fall. How
much lower will it be when it comes to rest?
Look at the answer.
© Copyright 1996 by
Eric Postpischil.
 Also note that the distance from A to C is six meters, and the distance from B
to D is six meters. This is important because we are going to connect seven
meters of rope from C to a point near A, and from B to a point near D. Since
each rope is longer than the six meter distance, the rope hangs slackly. The
new ropes are shown to the left (click
image for larger view).
Also note that the distance from A to C is six meters, and the distance from B
to D is six meters. This is important because we are going to connect seven
meters of rope from C to a point near A, and from B to a point near D. Since
each rope is longer than the six meter distance, the rope hangs slackly. The
new ropes are shown to the left (click
image for larger view).
 A weight is suspended from a fixed support by two springs and some rope as
shown in the diagram to the right
(click image for larger view). The
weight is two Newtons. (If you aren't metric, use pounds and feet instead of
Newtons and meters; the problem will work the same.) Each spring is one meter
long when unstretched, and it stretches two meters for every Newton of force on
it. The rope from B to C is one meter. Like all textbook physics problems, this
one uses ideal parts. In particular, the springs and ropes have no mass of
their own.
A weight is suspended from a fixed support by two springs and some rope as
shown in the diagram to the right
(click image for larger view). The
weight is two Newtons. (If you aren't metric, use pounds and feet instead of
Newtons and meters; the problem will work the same.) Each spring is one meter
long when unstretched, and it stretches two meters for every Newton of force on
it. The rope from B to C is one meter. Like all textbook physics problems, this
one uses ideal parts. In particular, the springs and ropes have no mass of
their own.